二叉搜索树—BST

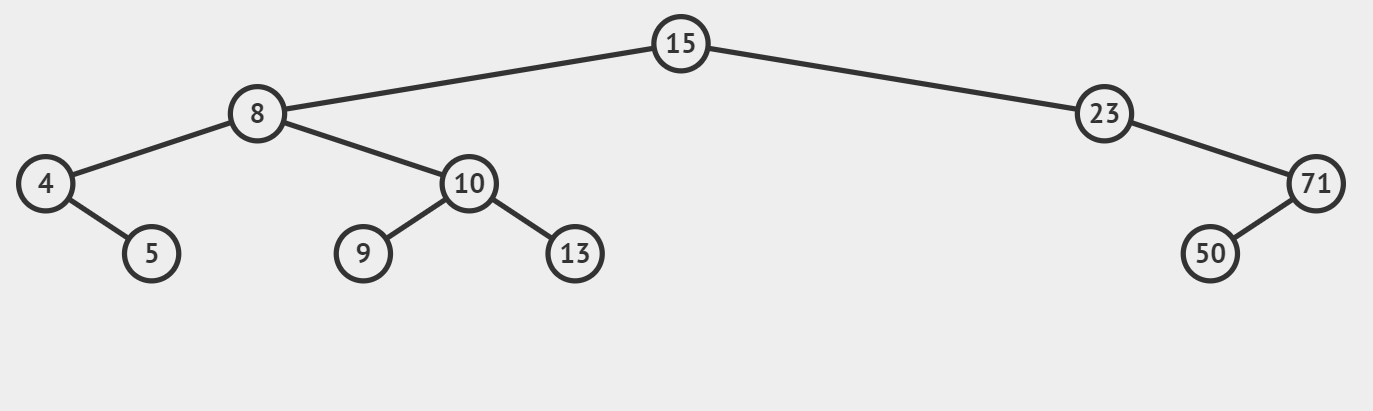
二叉搜索树又称二叉排序树(Binary Search Tree)，简称BST。主要用于查找搜索。

如果理解起来有些抽象，可以尝试这个网站，可视化演示操作过程：visualgo

定义

二叉搜索树或者为空树或者满足如下条件：

若左子树非空，左子树全部节点小于根节点
若右子树非空，右子树全部节点大于根节点
左右子树均满足以上两点（递归定义的）

二叉搜索树是没有重复元素的。

优势在于查找和插入，时间复杂度可以达到O(logn)。

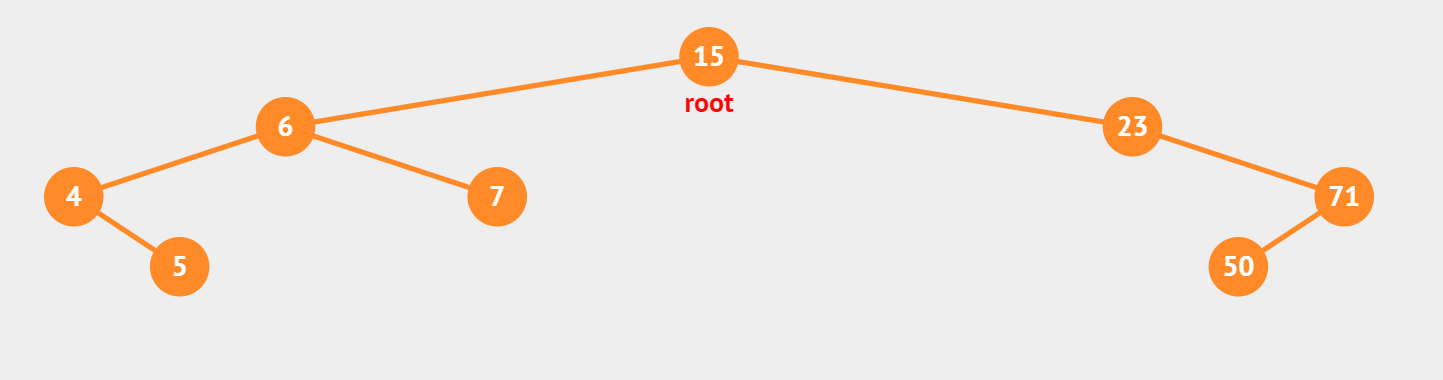
如上图即为一颗BST树。

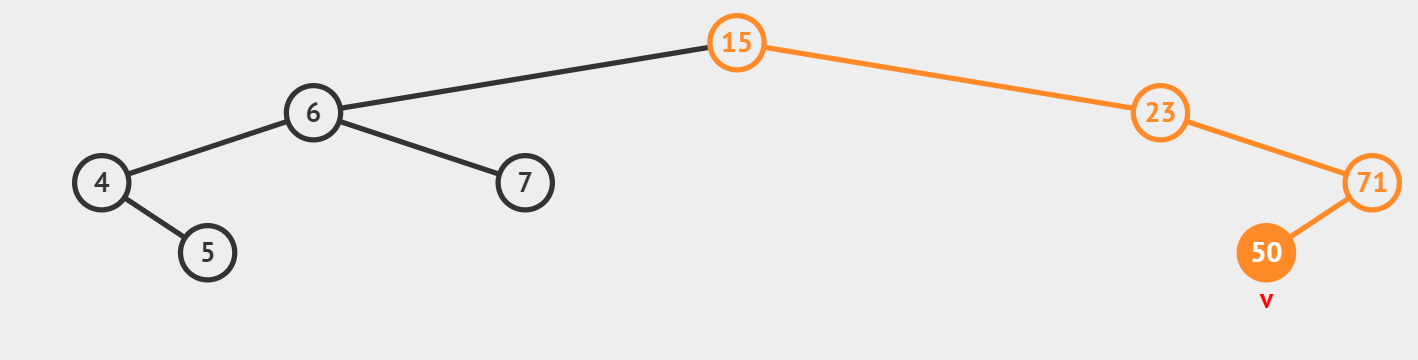
查找

如图为查找50的过程

从根节点开始，若节点为NULL，否则比较根节点与搜索值的大小关系，如果相等则查找成功，如果小于根节点值则转到左子树上继续查找，同理若大于节点值则转到右节点上继续查找。

BSTNode *BSTNode::findNode(int val)
{
    if (val == value)
        return this;
    else if (val < value)
    {
        if (left == NULL)
            return NULL;
        return left->findNode(val);
    }
    else if (val > value)
    {
        if (right == NULL)
            return NULL;
        return right->findNode(val);
    }
    return NULL;
}

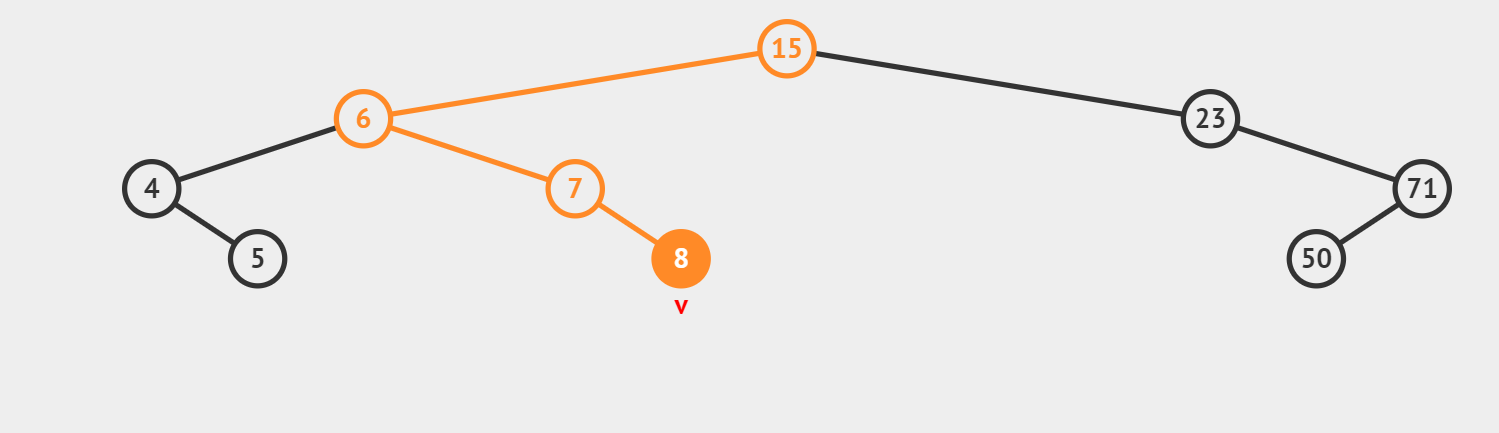
插入

如图为插入8的过程：

插入的关键是找到插入的位置, 可以在查找的基础上改装成插入，即若查找成功代表插入值已存在于BST中无需再次插入，查找失败（找到了NULL），则该位置即为需要插入的位置。

void BSTNode::insertNode(int val)
{
    if (val < value)
    {
        if (left == NULL)
        {
            left = new BSTNode(val);
            left->parent = this;
        }
        else
            left->insertNode(val);
    }
    else if (val > value)
    {
        if (right == NULL)
        {
            right = new BSTNode(val);
            right->parent = this;
        }
        else
            right->insertNode(val);
    }
}

删除

首先定义两个概念：

前驱结点：节点val值小于该节点val值并且值最大的节点
后继节点：节点val值大于该节点val值并且值最小的节点

相比较而言删除操作较为复杂，需要考虑多种情况：

假设待删除节点为d

若d为叶节点，则直接删除即可。
若节点只有左子树，则将左子树改为d父节点的子树。（右节点同理）
若d有两棵子树,则让d的后继（或者前驱）节点x取代d的位置，并将原位置的x删除掉（此时会转换成1或2的情况）

由于前两者情况较为简单，这里演示第三种情况：

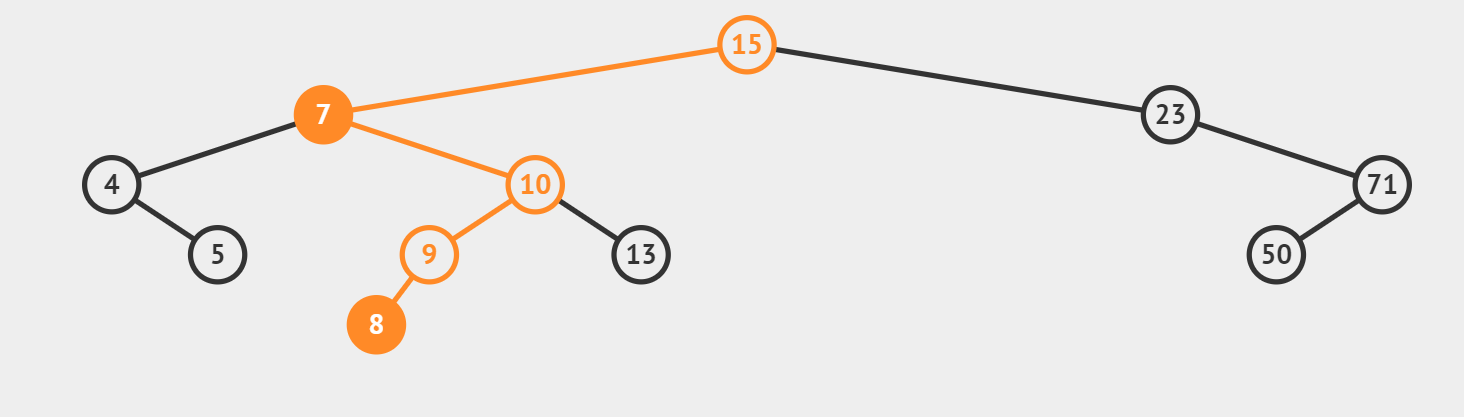
删除如图BST中值为7的节点：

首先查找到6：

然后发现6的左右子树均非空，这里选择右子树，查找到后继节点8

用8替代7的位置

由于8节点为叶节点，因此直接删除。


void BSTNode::delNode()
{
    if (left != NULL && right != NULL)
    {
        BSTNode *temp = left->findMax();
        value = temp->value;
        temp->delNode();
    }
    else
    {
        if (left == NULL)
        {
            if (this == parent->left)
            {
                parent->left = right;
            }
            else
            {
                parent->right = right;
            }
            if (right != NULL)
            {
                right->parent = parent;
            }
        }
        else
        {
            if (this == parent->left)
            {
                parent->left = left;
            }
            else
            {
                parent->right = left;
            }
            left->parent = parent;
        }
    }
}

完整代码

#include <bits/stdc++.h>
using namespace std;

class BSTNode
{
public:
    int value;
    BSTNode *left;
    BSTNode *right;
    BSTNode *parent;

public:
    BSTNode(int val);
    BSTNode *findNode(int val);
    void insertNode(int val);
    void delNode();
    BSTNode *findMin();
    BSTNode *findMax();
};

BSTNode *BSTNode::findMin()
{
    BSTNode *tmp = this;
    while (tmp->left != NULL)
        tmp = tmp->left;
    return tmp;
}

BSTNode *BSTNode::findMax()
{
    BSTNode *tmp = this;
    while (tmp->right != NULL)
        tmp = tmp->right;
    return tmp;
}
void BSTNode::delNode()
{
    if (left != NULL && right != NULL)
    {
        BSTNode *temp = left->findMax();
        value = temp->value;
        temp->delNode();
    }
    else
    {
        if (left == NULL)
        {
            if (this == parent->left)
            {
                parent->left = right;
            }
            else
            {
                parent->right = right;
            }
            if (right != NULL)
            {
                right->parent = parent;
            }
        }
        else
        {
            if (this == parent->left)
            {
                parent->left = left;
            }
            else
            {
                parent->right = left;
            }
            left->parent = parent;
        }
    }
}

BSTNode::BSTNode(int val)
{
    value = val;
    left = right = parent = NULL;
}
BSTNode *BSTNode::findNode(int val)
{
    if (val == value)
        return this;
    else if (val < value)
    {
        if (left == NULL)
            return NULL;
        return left->findNode(val);
    }
    else if (val > value)
    {
        if (right == NULL)
            return NULL;
        return right->findNode(val);
    }
    return NULL;
}
void BSTNode::insertNode(int val)
{
    if (val < value)
    {
        if (left == NULL)
        {
            left = new BSTNode(val);
            left->parent = this;
        }
        else
            left->insertNode(val);
    }
    else if (val > value)
    {
        if (right == NULL)
        {
            right = new BSTNode(val);
            right->parent = this;
        }
        else
            right->insertNode(val);
    }
}
/**
 * @brief
 *
 */
class BST
{
public:
    BST();
    BST(vector<int> v);
    BSTNode *find(int val);
    BSTNode *root;
    bool del(int val);
    void insert(int val);
};

BST::BST()
{
    root = NULL;
}
BST::BST(vector<int> v)
{
    root = NULL;
    for (int i = 0; i < v.size(); i++)
    {
        root->insertNode(v[i]);
    }
}
BSTNode *BST::find(int val)
{
    if (root == NULL)
        return NULL;
    else
        return root->findNode(val);
}
void BST::insert(int val)
{
    if (root == NULL)
        root = new BSTNode(val);
    else
    {
        root->insertNode(val);
    }
}
bool BST::del(int val)
{
    BSTNode *findNode = find(val);
    if (findNode == NULL)
        return false;
    if (findNode == root)
    {
        if (root->left == NULL && root->right == NULL)
        {
            root = NULL;
            delete findNode;
        }
        else if (root->left == NULL)
        {
            root = root->right;
            root->parent = NULL;
            delete findNode;
        }
        else if (root->right == NULL)
        {
            root = root->left;
            root->parent = NULL;
            delete findNode;
        }
        else
        {
            root->delNode();
        }
    }
    else
    {
        root->delNode();
    }
    return true;
}

创建

创建就是按顺序的插入过程

参考文档二叉搜索树BST在C++类中的实现（增删改查）【Van0512】